Quantitative Methods: Assignment 5

Correlation and Spatial Autocorrelation

Introduction:

This assignment incorporated learning and applying the following skills:

• Run Correlations in SPSS
• Interpret Correlation from a Scatterplot and SPSS Output
• Use the U.S. Census Site to Download Data and Shapefiles 
• Identify GEOIDs from the Census Data
• Join U.S. Census Data and other Data
• Create a report connecting all the data

In Part 1, the goal was to learn to create a correlation matrix in SPSS in order to analyze correlations between variables in a dataset.  The case study area for this part was Milwaukee, Wisconsin.  The data included race, economic, and occupation variables.  

In Part 2, the goal was to analyze patterns of the presidential elections from 1980 and 2016 from data given by the Texas Election Commission (TEC).  The TEC wants to determine if there are clustering of voting patterns in the state, as well as voter turnout, so that it can provide the information to the governor to see if election patterns have changed or not over 36 years.

Important terms:
Spatial Autocorrelation - correlation of a variable with itself through space.  If there is some systematic pattern in the spatial distribution of a variable, it is said to be spatially autocorrelated.

Moran's I - is used to compare the value of the variable at any one location with the value at all other locations.  It creates a chart that displays spatial autocorrelation.  

Local Indicators of Spatial Autocorrelation (LISA) - a map providing a spatial component of spatial autocorrelation that uses spatial weights to determine clustering.  Any colors on the LISA map are significant (p=0.05).

Methods:

Part 1:
Using SPSS, a correlation matrix was created from an excel file containing the data.  The chart in Figure 1 could then be analyzed to recognize any patterns in the data.

Part 2:
The first step in this part was to download the Texas shapefile from the U.S. Census, along with Hispanic data.  Once downloaded, the Hispanic data and voting data were joined to the Texas shapefile.  The shapfile was then exported so that it could be opened in Geoda.  In Geoda, a spatial weight was created because there is spatial autocorrelation for both elections, voter turnout, and hispanic populations.  Next a Moran's I and LISA Cluster Map were created for voter turnout for both elections and percent democratic vote for both elections.  Figures 2, 4, 6, and 8 show the Moran's I charts and Figures 3, 5, 7, and 9 show the corresponding LISA Cluster Maps.  These were then used to analyze patterns in the Texas elections in 1980 and 2016.


Results:

Part 1:

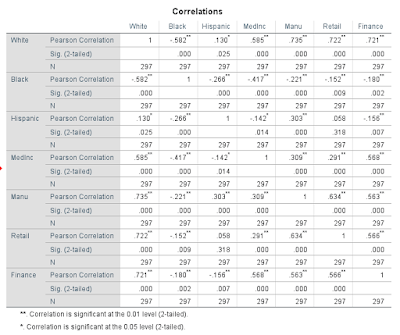Figure 1

Through analyzing the results from the correlation matrix, it can be observed that in Milwaukee, white populations have the strongest positive correlations with:  

-median household income – moderate correlation

·         -number of manufacturing employees – high correlation

·         -number of retail employees – high correlation

·         -number of finance employees – high correlation

What this means is that where there are higher populations of white people, these traits tend to be higher.  This means that whites hold most of the jobs and tend to have a higher median household income.  It should also be noted that in Milwaukee, black populations have all negative correlations with:

·         -median household income – low correlation

·        - number of manufacturing employees – little if any correlation

·         -number of retail employees – little if any correlation

·         -number of finance employees – little if any correlation

Though none of these are more than a low correlation, it can be compared to the same statistics for the white populations.  Just the fact that all these have a slightly negative correlation shows that where there are higher populations of black people, the median household income may tend to be lower, and they do not hold as many jobs as white people.  

Part 2:

Figure 2: Voter Turnout 1980

This chart shows that there was some positive spatial autocorrelation of voter turnout in the 1980 presidential election.

Figure 3: Voter Turnout 1980 LISA

It can be observed that voter turnout was low in the southern portion of the state, as well as in a cluster of counties on the eastern portion of the state.  Voter turnout was higher in the northern portion of the state, as well as in clusters near the center of the state.

Figure 4: Voter Turnout 2016

This chart shows that there was still some positive spatial autocorrelation of voter turnout in the presidential election in 2016, though it decreased since the 1980 election.

Figure 5: Voter Turnout 2016 LISA

It can be observed that voter turnout was lower in the southern portion of the state, just as in 1980, however there are now no counties on the eastern side of the state that had a significantly low voter turnout.  There are now a few counties scattered throughout the northwest and central portion of the state.  The state had a noticeable change in counties with high voter turnout; there are nearly half as many counties with a significantly high voter turnout.

Figure 6: Percent Democrat 1980

This chart shows that there was a positive spatial autocorrelation of the percent democratic vote in the 1980 presidential election.

Figure 7: Percent Democrat 1980 LISA

The west-central and north-western part of the state had a large area with a significantly low percent democratic vote.  The southern portion of the state saw a large area with a high percent democratic vote, as well as a few counties on the eastern side of the state.

Figure 8: Percent Democrat 2016

This chart shows that there was a positive spatial autocorrelation of percent democratic vote in the 2016 presidential election, and it was an increase from the 1980 election.

Figure 9 Percent Democrat 2016 LISA

The area of the low percent democratic vote shifted to the center and the north part of the state, while the southern portion of the state stayed about the same with a high percent democratic vote.  Now however, there is only one county near the eastern side of the state with a high percent democratic vote.  The western side of the state gained a handful of counties with a significantly high percent democratic vote.


Conclusion:
There is observable clustering of voting patterns in both the 1980 and 2016 presidential elections in the state of Texas.  These patterns have also changed over the course of 36 years.  In general, the southern portion of the state has had a lower voter turnout with a high percent democratic vote, and the northern portion of the state has had a higher voter turnout with a low percent democratic vote.  The Moran's I charts show that spatial clustering occurred in all the elections in both voter turnout and counties with high or low percent democratic vote.  The clustering was more prevalent in using the percent democratic vote variable, and this is also visible in the LISA maps.  This study truly helped display Tobler's Law (the first law of geography): everything is related to everything else, but near things are more related than distant things.


Sources:

-Data acquired from the U.S. Census Bureau and voting data acquired from instructor
-ArcMap used to join tables to shapefile
-Geoda was used to create Moran's I and Lisa Cluster Maps
-IBM SPSS Statistics 24 used to create correlation matrix